二分探索
二分探索、例題、テンプレート、ノート https://www.youtube.com/watch?v=v57lNF2mb_s
二分探索
この問題の元の形は:配列が与えられ、ある数がこの配列内に存在するかどうかを調べ、その位置を返すというものです。
明らかな特徴:入力はソート済みで重複がない。
二分探索は実際に配列を3つの部分に分割します。まずその数が中間のものかどうかを確認し、そうでなければサイズに基づいて左半分または右半分を検索します。毎回配列全体を半分にします。
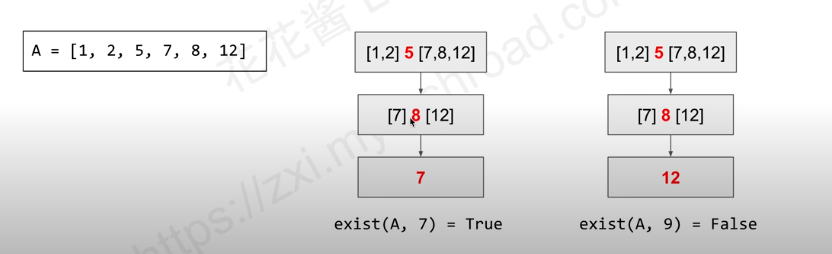
二分探索の非常に明らかな特徴は速いことです。
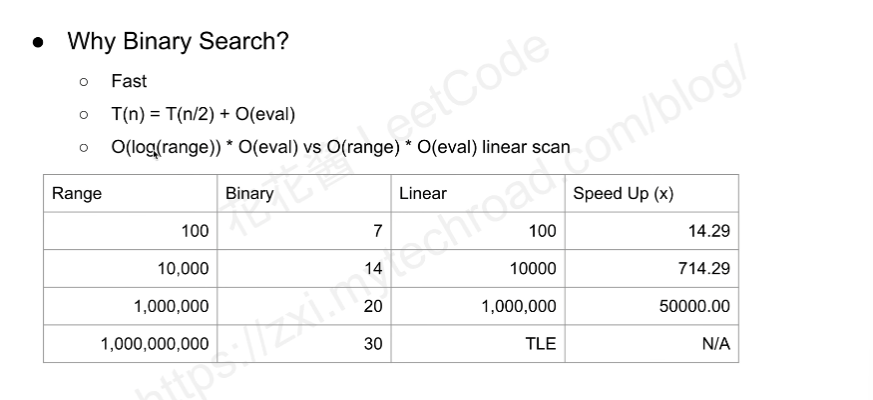
テンプレート:
#[l,r)
def binary_search(l,r);
while l<r:
m=l+(r-1)//2 # 中間の数を取得
if f(m):return m # オプション:この数が解かどうかを判断
if g(m): # 解の範囲が左か右かを判断
r=m # 新しい範囲[1,m) 左側
else:
l=m+1 #[m+1,r)
return l # または見つからない例えば、C++版:
class Solution
{
public:
int search(vector<int> &nums, int target)
{
int left = 0;
int right = nums.size(); // targetを左閉右開区間で定義:[left, right)
while (left < right)
{ // left == rightの時、[left, right)は無効な空間なので < を使用
int middle = left + ((right - left) >> 1);
if (nums[middle] == target)
{
return middle;
}
if (nums[middle] > target)
{
right = middle; // targetは左区間、[left, middle)内
}
else if (nums[middle] < target)
{
left = middle + 1; // targetは右区間、[middle + 1, right)内
}
}
// 目標値が見つからない
return -1;
}
};配列の値が一意でない場合、STLの2つの関数を使用できます:
lower_boundは配列内でx以上の最初の要素を見つけます
upper_boundは配列内でxより大きい最初の要素を見つけます
lower_bound(first,last,val) [first,last)
見つからない場合、その要素が存在した場合の位置を返します。
変形問題
LeetCode 69
#include<math.h>
using namespace std;
class Solution {
public:
int mySqrt(int x) {
int right=sqrt(x);
int left = 0; // targetを左閉右開区間で定義:[left, right)
while (left < right)
{ // left == rightの時、[left, right)は無効な空間なので < を使用
int middle = left + ((right - left) >> 1);
if (middle< right)
{
left = middle + 1; // targetは右区間、[middle + 1, right)内
}
}
return left;
}
};やった!自分で解けた!
LeetCode 278
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);
class Solution {
public:
int firstBadVersion(int n) {
int left = 1;
int right = n; // targetを左閉右開区間で定義:[left, right)
int middle=0;
while (left < right)
{ // left == rightの時、[left, right)は無効な空間なので < を使用
middle = left + ((right - left) >> 1);
if (isBadVersion(middle) ){
right = middle;
// targetは左区間、[left, middle)内
}
else
{
left = middle+1 ; // targetは右区間、[middle + 1, right)内
}
}
/*左開右閉なので、最後の一つが悪いかどうか確認が必要
この時点で、left>=rightまで絞り込まれている
例えば、全部で5つあり4番目が悪い場合、leftは4、rightも4、4はfalse
最初が悪い場合、leftはrightより大きい
*/
if(isBadVersion(right))
{
return right;
}
else
{return middle;}
}
};やった!また自分で解けた!
LeetCode 875 - 初めて自分でmedium問題に挑戦。
やはり解けなかった。
この問題はバナナを食べる速度をH(時間)に変換する必要があります。
Kが与えられた時、食べ終わるのに何時間かかるか?
class Solution {
public:
int minEatingSpeed(vector<int>& piles, int H) {
int low = 1, high = 1000000000, k = 0;
while (low <= high) {
k = (low + high) / 2;
int h = 0;
for (int i = 0; i < piles.size(); i ++)
h += ceil(1.0 * piles[i] / k);
if (h > H)
low = k + 1;
else
high = k - 1;
}
return low;
}
};注意点はceil(1.0 * piles[i] / k) - これはi番目の山を食べるのに必要な時間です。食べ終わったらもう食べないので、ceilを使用しています。
別の変形 - 378
またmedium問題。
アイデアがない。
あ、なるほど - 自分の数より小さい数がいくつあるか確認する。
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
class Solution {
public:
int kthSmallest(vector<vector<int>>& matrix, int k) {
int n = matrix.size();
int left = matrix[0][0];
int right = matrix[n - 1][n - 1];
while(left < right) {
int mid = left + (right - left) / 2;
int res = 0;
for(int i = 0; i < n; i++) {
res += upper_bound(matrix[i].begin(), matrix[i].end(), mid) - matrix[i].begin();
}
if(res < k) {
left = mid + 1;
}else {
right = mid;
}
}
return left;
}
};このアイデアはupper_boundを使用して、中間値より小さい数がいくつあるかを数えることです。
各行に対して、upper_boundを実行します。パラメータはこの行の最初の値、この行の最後の値、そして行列全体の中間値です。
upper_boundは行列の中間値より大きい最初の要素のインデックスを返します。
このインデックスがkより小さい場合、行列の中間値がまだ十分大きくない、つまり答えは右側にあることを意味します。
等しくなったら終了なので、直接leftを返します。
まとめ:この種の問題で最も重要なのはg(m)を見つけることです。残りはテンプレートを適用するだけです。