Scipy optimize
この記事では主によく使われる関数を紹介します:
minimize
Least_square
nnls
Lsq_linear
Curve_fit
また、numpy.linalg.lstsqも紹介します。
また、興味深いことを発見しました。一般的にxを関数の最初のパラメータにしないとフィッティングがうまくいきません。
minimize
これは主にMATLABのfminuncを置き換えるために使用されます。
scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)funは最小化するコスト関数です。コスト関数の要件は:
fun
The objective function to be minimized.
fun(x, *args) -> float
where x is an 1-D array with shape (n,) and args is a tuple of the fixed parameters needed to completely specify the function.
x0は初期パラメータ、つまり一般的に言う初期推定値です。Array of real elements of size (n,), where ‘n’ is the number of independent variables.
method:このパラメータは使用する方法を表します。デフォルトはBFGS、L-BFGS-B、SLSQPのいずれかで、TNCも選択可能です。
jacは勾配を計算する方法で、ほとんどの場合無視できます。これはヤコビ行列です。
options:最大反復回数を制御するために使用され、辞書形式で設定します。例:options={‘maxiter’
}boundssequence or
Bounds, optionalBounds on variables for L-BFGS-B, TNC, SLSQP, Powell, and trust-constr methods. There are two ways to specify the bounds:
- Instance of
Boundsclass.- Sequence of
(min, max)pairs for each element in x. None is used to specify no bound.constraints{Constraint, dict} or List of {Constraint, dict}, optional
Constraints definition (only for COBYLA, SLSQP and trust-constr).
Constraints for ‘trust-constr’ are defined as a single object or a list of objects specifying constraints to the optimization problem. Available constraints are:
boundsは主に上下限を制御するために使用され、constraintsは変数間の関係を通じて範囲を狭めます。
tol: float, optional
Tolerance for termination. For detailed control, use solver-specific options.
tolは最小反復値で、反復を停止する条件です。
以下はRosenbrock関数の例です:
import numpy as np
from scipy.optimize import minimize
def rosen(x):
"""The Rosenbrock function"""
return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead',
options={'xatol': 1e-8, 'disp': True})
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 339
Function evaluations: 571
>>>
print(res.x)
[1. 1. 1. 1. 1.]多くの場合、境界や制約を使用する必要があります。ここでは境界を示します。
Least_square
scipy.optimize.least_squares(fun, x0, jac='2-point', bounds=- inf, inf, method='trf', ftol=1e-08, xtol=1e-08, gtol=1e-08, x_scale=1.0, loss='linear', f_scale=1.0, diff_step=None, tr_solver=None, tr_options={}, jac_sparsity=None, max_nfev=None, verbose=0, args=(), kwargs={})これは前のものとほぼ同じです。
nnls
scipy.optimize.nnls(A, b, maxiter=None)x>=0の条件でargmin_x || Ax - b ||_2を解きます。
パラメータ
**A **ndarray
上記の行列
A。**b ** ndarray
右辺ベクトル。
maxiter: int, optional
最大反復回数、オプション。デフォルトは
3 * A.shape[1]。
戻り値
**x ** ndarray
解ベクトル。
**rnorm: float
残差、
|| Ax-b ||_2。
lsq_linear
scipy.optimize.lsq_linear(A, b, bounds=- inf, inf, method='trf', tol=1e-10, lsq_solver=None, lsmr_tol=None, max_iter=None, verbose=0)変数に境界を持つ線形最小二乗問題を解きます。
m×nの設計行列Aとm個の要素を持つ目標ベクトルbが与えられた場合、lsq_linearは以下の最適化問題を解きます:
minimize 0.5 * ||A x - b||**2
subject to lb <= x <= ubcurve_fit
scipy.optimize.curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=True, bounds=- inf, inf, method=None, jac=None, **kwargs)これは実際に最もよく使われる関数です。
ここでのfはコスト関数ではなく、モデル関数であることに注意してください。例えば:
def f_1(x, A, B):
return A * x + B- **xdata array_like or object **データが測定される独立変数。通常はM長のシーケンスまたはk個の予測子を持つ関数の(k,M)形状の配列ですが、実際には任意のオブジェクトにできます。 簡単に言えば、フィッティングする独立変数の配列です。
- **ydata array_like **従属データ、長さMの配列 - 名目上は
f(xdata,...)。 簡単に言えば、フィッティングする従属変数の値の配列です。 - p0 array_like , optionalパラメータの初期推定値(長さN)。Noneの場合、初期値はすべて1になります。 関数のパラメータに初期値を設定して計算量を減らします。
- 最適化に使用する方法。詳細は
least_squaresを参照。
以下は公式の例です:
import matplotlib.pyplot as plt
from scipy.optimize import curve_fitdef func(x, a, b, c):
return a * np.exp(-b * x) + cノイズを含むフィッティングデータを定義:
xdata = np.linspace(0, 4, 50)
y = func(xdata, 2.5, 1.3, 0.5)
np.random.seed(1729)
y_noise = 0.2 * np.random.normal(size=xdata.size)
ydata = y + y_noise
plt.plot(xdata, ydata, 'b-', label='data'関数funcのパラメータa、b、cをフィッティング:
popt, pcov = curve_fit(func, xdata, ydata)
popt
plt.plot(xdata, func(xdata, *popt), 'r-',
label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))最適化を0 <= a <= 3、0 <= b <= 1、0 <= c <= 0.5の範囲に制約:
popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5]))
popt
plt.plot(xdata, func(xdata, *popt), 'g--',
label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()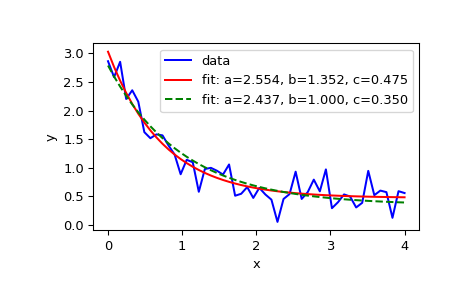
しかしここで問題があります:aの値を固定したい場合、または各関数が固定されたaの値を持つ一連の関数を取得したい場合はどうすればよいでしょうか?
この場合、aを変数として扱わず、別の関数を作成してaを渡す必要があります。例えば:
custom_gaussian = lambda x, mu: gaussian(x, mu, 0.05)lambdaを使用して小さな無名関数を作成します:
import matplotlib.pyplot as plt
import numpy as np
import scipy.optimize
def gaussian(x, mu, sigma):
return 1 / sigma / np.sqrt(2 * np.pi) * np.exp(-(x - mu)**2 / 2 / sigma**2)
# これは元の完全なパラメータを持つガウス関数です
# サンプルデータを作成
x = np.linspace(0, 2, 200)
y = gaussian(x, 1, 0.1) + np.random.rand(*x.shape) - 0.5
plt.plot(x, y, label="sample data")
# 元のフィット関数でフィッティング
popt, _ = scipy.optimize.curve_fit(gaussian, x, y)
plt.plot(x, gaussian(x, *popt), label="gaussian")
# 固定された`sigma`を持つカスタムフィット関数でフィッティング
custom_gaussian = lambda x, mu: gaussian(x, mu, 0.05)
# これはフィッティングしたいカスタマイズされたガウス関数です
popt, _ = scipy.optimize.curve_fit(custom_gaussian, x, y)
plt.plot(x, custom_gaussian(x, *popt), label="custom_gaussian")
plt.legend()
plt.show()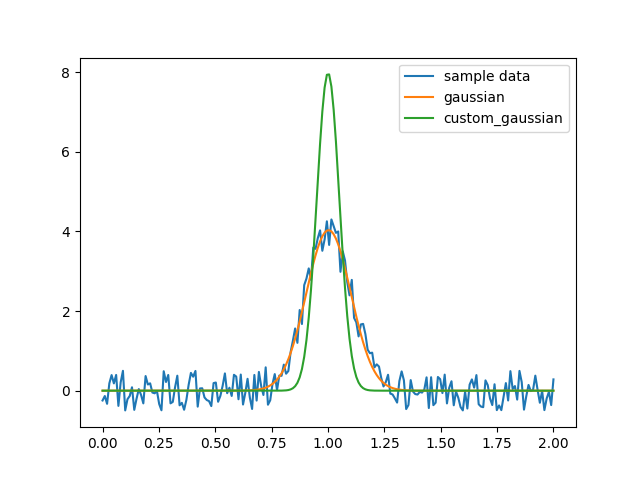
numpy.linalg.lstsq
これはnumpyに組み込まれた線形行列方程式の最小二乗解です。
ここで線形方程式系の問題を思い出す必要があります:
(この大括弧のフォーマットには問題があるかもしれません)
ここでおよびなどは既知の定数であり、などは求める未知数です。
線形代数の概念を使用すると、線形方程式系は次のように書けます:
ここでAはm×n行列、xはn個の要素を持つ列ベクトル、bはm個の要素を持つ列ベクトルです。
x1、x2、……xnの組が方程式系のすべての等式を成り立たせる場合、この組を方程式系の解と呼びます。線形方程式系のすべての解の集合は解集合と呼ばれます。解の存在に基づいて、線形方程式系は3つのタイプに分類できます:
一意の解を持つ正定方程式系、
解が存在しない過剰決定方程式系、
無限に多くの解を持つ不足決定方程式系(不定方程式系とも呼ばれます)。
線形代数は基本的に、解が存在するかどうかの判定方法と解の求め方の2つを扱います。
線形方程式系の復習については線形方程式PDFを参照してください。
厳密ではありませんが、m>nの場合は一般的に解がなく、過剰決定方程式系と呼ばれます。しかしこの場合、問題を最適化問題に変換できます:を最小化するxの組を見つけます。これが最小二乗問題です。
パラメータ
a(M, N) array_like
「係数」行列。
b{(M,), (M, K)} array_like
縦座標または「従属変数」の値。bが2次元の場合、bのK列それぞれに対して最小二乗解が計算されます。
rcondfloat, optional
aの小さな特異値のカットオフ比率。ランク決定の目的で、特異値がaの最大特異値のrcond倍より小さい場合、ゼロとして扱われます。
戻り値
x{(N,), (N, K)} ndarray
最小二乗解。bが2次元の場合、解はxのK列にあります。
residuals{(1,), (K,), (0,)} ndarray
残差の合計;
b - a*xの各列のユークリッド2ノルムの二乗。aのランクが< Nまたは M <= Nの場合、これは空の配列です。rankint
行列aのランク。
s(min(M, N),) ndarray
aの特異値。
の例
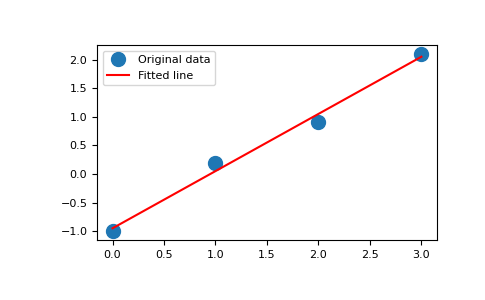
x = np.array([0, 1, 2, 3]) y = np.array([-1, 0.2, 0.9, 2.1])
係数を調べると、直線の傾きはおよそ1で、y軸との交点はおよそ-1であることがわかります。
直線の方程式をy = Apと書き換えることができます。ここでA = [[x 1]]、p = [[m], [c]]です。lstsqを使用してpを解きます:
A = np.vstack([x, np.ones(len(x))]).T
>>> A
array([[ 0., 1.],
[ 1., 1.],
[ 2., 1.],
[ 3., 1.]])m, c = np.linalg.lstsq(A, y, rcond=None)[0]
>>> m, c
(1.0 -0.95) # may varyimport matplotlib.pyplot as plt
>>> _ = plt.plot(x, y, 'o', label='Original data', markersize=10)
>>> _ = plt.plot(x, m*x + c, 'r', label='Fitted line')
>>> _ = plt.legend()
>>> plt.show()