Life Odyssey

Binary search

6 min

二分查找，例题，模板，笔记https://www.youtube.com/watch?v=v57lNF2mb_s

二分查找

这个题最初的样子是，给一个数组，让你查找某个数是否在这个数组内并且返回位置

一个明显的特点 输入是排好序并且不重复的。

二分查找实际上是把数组划分为三部分，先看这个数字是不是中间那个，不是的话就去根据大小搜索左半部分，每次都把整个数组减半

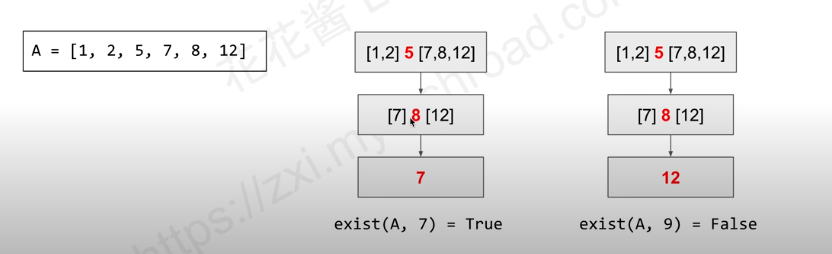
image-20220310125224057
image-20220310125224057

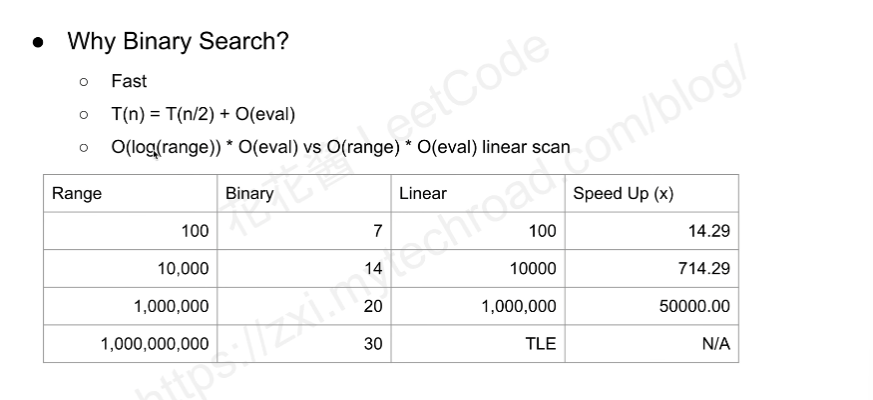
二分查找的一个很明显的特点就是快

image-20220310125353351
image-20220310125353351

一个模板

#[l,r)
def binary_search(l,r);
	while l<r:
        m=l+(r-1)//2#取出中间的数
        if f(m):return m#optional 判断这个数是不是我的解
        if g(m):#判断解的范围是在左边还是右边
            r=m# new range[1,m)左边
        else:
            l=m+1#[m+1,r)
  return l# or not found

比如说一个c++的

class Solution
{
public:
    int search(vector<int> &nums, int target)
    {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right)
        { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if  (nums[middle] == target)
            {
                return middle;
            }
            if (nums[middle] > target)
            {
                right = middle; // target 在左区间，在[left, middle)中
            }
            else if (nums[middle] < target)
            {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            }

        }
        // 未找到目标值
        return -1;
    }
};

如果数组的值不是唯一的，可以使用stl里面的两个函数

lower_bound找到数组里面第一个大于等于x

upper_bound找到数组里面第一个大于x

lower_bound(first,last,val) [fisrt,last)

如果没有，则返回假设该元素存在的时候该元素的位置

变种题

LeetCode 69

#include<math.h>
using namespace std;
class Solution {
public:
    int mySqrt(int x) {
        int right=sqrt(x);
        int left = 0; // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right)
        { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);

            if (middle< right)
            {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            }

        }
        return left;
    }
    
};

好耶 我自己做出来了

leetcode 278

// The API isBadVersion is defined for you.
// bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
        int left = 1;
        int right = n; // 定义target在左闭右开的区间里，即：[left, right)
        int middle=0;
        while (left < right)
        { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            middle = left + ((right - left) >> 1);
            if (isBadVersion(middle) ){

                right = middle; 
             // target 在左区间，在[left, middle)中
            }
            else 
            {
                left = middle+1 ; // target 在右区间，在[middle + 1, right)中
            }

            
    }
        /*因为是左开右闭，需要判断最后一个会不会是坏的
        因为到了现在这个情况，已经缩小到left>=right了
        就比如 一共五个，第四个坏了的话，这个时候left是4，right也是4，4是false。
        如果是第一个就坏了，这个时候left是比right大的
        如果
        */
            if(isBadVersion(right))
            {
                return right;
            }
        else
        {return middle;}
    }
};

好耶 又是我自己做出来的

LeetCode875 第一次自己做medium

果然没做出来。

这题需要把吃香蕉的速度转化为H。

即给定K，吃完需要多少时间

class Solution {
public:
    int minEatingSpeed(vector<int>& piles, int H) {
        int low = 1, high = 1000000000, k = 0;
        while (low <= high) {
            k = (low + high) / 2;
            int h = 0;
            for (int i = 0; i < piles.size(); i ++) 
                h += ceil(1.0 * piles[i] / k);
            if (h > H)
                low = k + 1;
            else
                high = k - 1;
        }
        return low;
    }
};

一个需要注意的地方是ceil(1.0 * piles[i] / k) 这是吃掉第i块需要的时间，吃完之后就不吃了，所以用了ceil

另一个变形 378

又是一道medium

没有思路

哦哦，看一下有多少个数比我的这个数要小

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
class Solution {
public:
    int kthSmallest(vector<vector<int>>& matrix, int k) {
        int n = matrix.size();
		int left = matrix[0][0];
        int right = matrix[n - 1][n - 1];
    
        while(left < right) {
            int mid = left + (right - left) / 2;
                
            int res = 0;
            for(int i = 0; i < n; i++) {
                 res += upper_bound(matrix[i].begin(), matrix[i].end(), mid) - matrix[i].begin();
                
            }
            
            if(res < k) {
                    left = mid + 1;
            }else {
                    right = mid;
            }
        }
        
        return left;
    }
};

这个思路是利用upper bound 计算前面有多少个比中间值要小

就是说 我对每一行，做一个upper bound 参数分别是这一行的第一个值，这一行的最后一个值，以及整个矩阵的中间值。

upper bound会返回会第一个大于矩阵中间值的下标。

如果这个下标比k小，则证明矩阵中间值还不够，也就是说这个值还在右边

因为这个结束肯定是==就直接回left了

总结 这类题目最重要的是找到g（m）剩下的就都是套用模板了

Algorithm LeetCode